WEEK OF APRIL 18-22, 2016

FALCONS,

WE HAD A GREAT WEEK FULL OF LEARNING AND DEDICATION.

THIS WEEK WE WILL BE WORKING WITH DEPENDENT AND INDEPENDENT VARIABLES,WRITING EQUATIONS FROM TABLES AND GRAPHS, AREA, PERIMETER, AND VOLUME OF DIFFERENT SHAPES.WE WILL ALSO BE EXPLORING DIFFERENT TRIANGLE PROPERTIES AND ATTRIBUTES.

WE HAVE 15 MORE SCHOOL DAYS FOR STAAR!  MAKE SURE YOU CONTINUE COMING TO MATH DURING RECESS FOR EXTRA HELP AND BE PRESENT FOR SATURDAY TUTORIALS. 

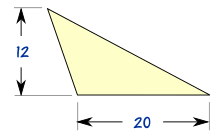
Area of Triangles Without Right Angles

There are several ways to find the area of a triangle.

Knowing Base and Height

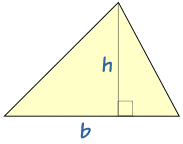
When we know the base and height it is easy.

It is simply half of b times h

Area =	1	bh
	2

(The Triangles page explains more)

Example: What is the area of this triangle?

(Note: 12 is the height, not the length of the left-hand side)

Height = h = 12

Base = b = 20

Area = ½ bh = ½ × 20 × 12 = 120

Question 1 Question 2 Question 3 Question 4  

Knowing Three Sides

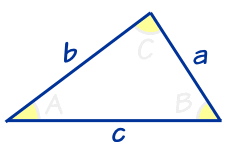There's also a formula to find the area of any triangle when we know the lengths of all three of its sides. This can be found on the Heron's Formula page.

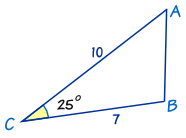
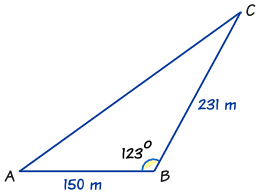
Knowing Two Sides and the Included Angle

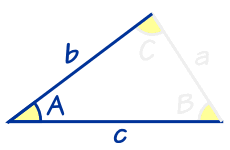When we know two sides and the included angle (SAS), there is another formula (in fact three equivalent formulas) we can use.

Depending on which sides and angles we know, the formula can be written in three ways:

Either:   Area = 1 ab sin C 2

Or:   Area = 1 bc sin A 2

Or:   Area = 1 ca sin B 2

They are really the same formula, just with the sides and angle changed.

Example: Find the area of this triangle:

First of all we must decide what we know.

We know angle C = 25º, and sides a = 7 and b = 10.

So let's get going:

Start with:		Area =	(½)ab sin C
Put in the values we know:		Area =	½ × 7 × 10 × sin(25º)
Do some calculator work:		Area =	35 × 0.4226...
		Area =	14.8 to one decimal place

How to Remember

Just think "abc": Area = ½ a b sin C

How Does it Work?

Well, we know that we can find an area when we know a base and height:

Area = ½ × base × height

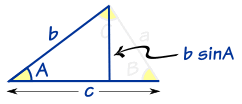In this triangle: the base is: c the height is: b × sin A

Putting that together gets us:

Area = ½ × (c) × (b × sin A)

Which is (more simply):

Area =	1	bc sin A
	2

By changing the labels on the triangle we can also get:

• Area = ½ ab sin C
• Area = ½ ca sin B

One more example:

Example: Find How Much Land

Farmer Jones owns a triangular piece of land.

The length of the fence AB is 150 m. The length of the fence BC is 231 m.

The angle between fence AB and fence BC is 123º.

How much land does Farmer Jones own?

First of all we must decide which lengths and angles we know:

• AB = c = 150 m,
• BC = a = 231 m,
• and angle B = 123º

So we use:

Area =	1	ca sin B
	2

Start with:		Area =	½ ca sinB
Put in the values we know:		Area =	½ × 150 × 231 × sin(123º) m2
Do some calculator work:		Area =	17,325 × 0.838... m2
		Area =	14,530 m2

Farmer Jones has 14,530 m² of land

REMINDERS:                                                                     

MONDAY-SPRING PICTURES

WEDNESDAY-WEAR BLUE OF SUPPORT OF AUTISM AWARENESS.

FRIDAY-PIZZA PARTY FOR STUDENTS THAT EARNED A LEVEL III ON MATH BENCHMARK.

PLEASE TRY YOUR BEST TO BE HERE EVERYDAY!

BE AWESOME!